Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
P1 - 4.
Un vagón de juguete con masa de $7{,}00 \mathrm{kg}$ se mueve en línea recta sobre una superficie horizontal sin fricción. Tiene una rapidez inicial de $4{,}00 \mathrm{m} / \mathrm{s}$ y luego es empujado a lo largo de $3 \mathrm{m}$, en la dirección de la velocidad inicial, por una fuerza cuya magnitud es de $10{,}0 \mathrm{N}$.
a) Use el teorema de trabajo y energía para calcular la rapidez final del vagón.
a) Use el teorema de trabajo y energía para calcular la rapidez final del vagón.
Respuesta
Arrancamos con un esquemita de la situación:
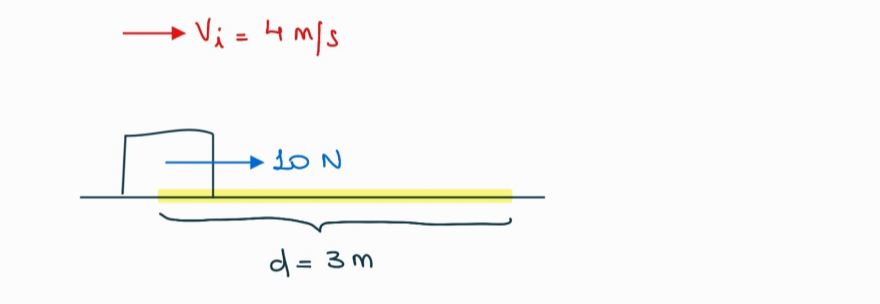
Reportar problema

Para calcular la velocidad final del vagón, vamos a usar que...
$W_{Tot} = \Delta E_c = E_{c_f} - E_{c_i}$
La única fuerza que está ejerciendo trabajo es la fuerza $F = 10 \text{ N}$ (el peso y la normal son perpendiculares a la dirección del movimiento, así que por esas no nos preocupamos, no realizan trabajo en este caso)
$|W_F| = 3 \text{ m} \cdot 10 \text{ N} = 30 \text{ J}$
Como el sentido de $F$ es el mismo que el del movimiento, este trabajo es positivo
$W_F = 30 \text{ J}$
Y como es la única fuerza ejerciendo trabajo en este caso, tenemos que...
$W_{Tot} = 30 \text{ J}$
Entonces, volviendo...
$W_{Tot} = E_{c_f} - E_{c_i}$
$30 \text{ J} = \frac{1}{2} \cdot m \cdot (V_f)^2 - \frac{1}{2} \cdot m \cdot (V_i)^2$
Saco factor común $\frac{1}{2} \cdot m$
$30 \text{ J} = \frac{1}{2} \cdot m \cdot [(V_f)^2 - (V_i)^2]$
Reemplazo por los datos que conozco, la masa $m$ y la velocidad inicial $V_i$
$30 \text{ J} = \frac{1}{2} \cdot 7 \text{ kg} \cdot [(V_f)^2 - (4 \, \frac{m}{s})^2]$
Ahora hay que despejar $V_f$ -> Por favor que no te confundan las unidades en este despeje! Tenemos todo en el SI, se las podemos sacar sólo para el despeje y ya sabemos que esa velocidad final la vamos a obtener en $m/s$
La ecuación a despejar, sin unidades ahora, nos queda así:
$30 = \frac{1}{2} \cdot 7 \cdot [(V_f)^2 - (4)^2]$
Ahora si, a despejar...
$30 = \frac{7}{2} \cdot [(V_f)^2 - 16]$
$\frac{60}{7} = (V_f)^2 - 16$
$\sqrt{\frac{60}{7} + 16} = V_f$
$V_f = 4.96 \, \frac{m}{s}$
Por lo tanto, la velocidad final del vagón es $4.96 \, \frac{m}{s}$
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
